ハートランド 2011

12/12 n進法　11/11 12回裏　10/10 習うよりも慣れろ　09/09 プラネタリウム　08/08 学習法　07/07 ライバル　06/06 継続すること　05/05 道具　04/04 研修　03/03 月明かりの中で　02/02 保険　01/01 サービス業

11/12/12
n進法

ふだん使っている数はいわゆる十進法です。これはヒトの指が十本あることに由来しているようです。「指折り数える」という表現があるように，ものを数えるときの自然な行為のひとつとして指を使う方法があるのでしょう。数字の記数法も算用数字である『0，1，2，3，…，9』を用いるのが一般的で，日本人ならば漢数字は時々使うでしょうが，特別でない限りはローマ数字を用いることはないでしょう。

ふだんの生活の中では十進法以外にも使っているものがあります。主なものとしては十二進法と六十進法です。どちらも時間に大きな関わりを持ちます。「午前9時の6時間後は」という問に「午後3時」と答えるにはそれほど時間は要さないでしょう。これをわざわざ十進法に直して計算する人はよほどの変わり者としか思えません。また「3時48分から26分経つと何時何分でしょう」の問題には「4時14分」と答えるでしょう。この問題の場合，解答の手順としてはまず『３時48分から４時までは12分』と考え，次に『26－12＝14』と計算すると答が出ます。この計算では3時48分に12分を足すと4時に『繰り上がる』ところがポイントです。でも，時計の計算方法を教わったばかりの小学生ならいざ知らず，大人にとってこの計算はそれほど難しいものではないでしょう。それだけ生活の中に時間が密着しているからです。その観点からすると，週や月あるいは年が変わるときの計算も同様でしょう。12月28日の一週間後が何月何日かを計算するときに，十進法を持ち出すのがいかにナンセンスかは容易に解ることでしょう。

コンピュータの世界が二進法であることはよく知られています。『0と1』だけのいわゆるデジタルの世界です。そのほかにも十六進法や1バイト＝8ビットのように八進法も用いられます。そろばんも一種のコンピュータであるという考え方があります。そろばんの場合，基本的には十進法と同じ作りですが，正確には二・五進法という2つのものが混ざっています。上の珠(たま)は下の4つ珠がいっぱいになるときに使われます。こうした二進法や五進法，あるいは十進法は総称してn進法と呼ばれます。来年から変わる数学の指導要領では高校一年でこのn 進法の単元が加わります。n進法の計算を考えることにより，これまでの常識である十進法の世界が打ち破られます。学ぶ側にとってはもどかしくもあり衝撃的でもあるでしょう。数の新しい世界を知るには年齢は関係ありません。二進法どうしの加減剰余をするとどんなことが起こるのか，デジタルの世界を一度のぞいてみてはいかがでしょうか。

11/11/11
12回裏

　日本のプロ野球では，以前はセ・パ両リーグの優勝チームが日本シリーズで決戦をし，日本一を決定する戦いをしていました。それぞれのリーグが年間140試合以上の長き戦いを勝ち抜いた結果，リーグで最高勝率を納めたチームが代表となるので，誰の目にも勝者が明らかでした。短期決戦をレベルの高いプロの選手達がプライドを賭けて戦う姿は，ペナントレースとはまた違った楽しみ方が出来ます。

そのリーグの代表を決めるシステムが，数年前から変わりました。セリーグとパリーグとではその開始時期は少し異なりましたが，いまは両リーグとも同じように実施されています。「クライマックスシリーズ」と呼ばれるもので，各リーグの上位３チームで争われます。まず最初に下位２チームが３試合戦う「ファーストステージ」があります。ここでは２勝した方が次に勝ち進みます。ただし，引き分けの場合は上位のチームすなわち２位のチームに有利にはたらきます。例えば１勝１敗１引き分けで終わった場合，２位のチームが勝ち進むのです。その後リーグの代表を決める「ファイナルステージ」が開催されるのです。ここでは１位のチームにアドバンテージが与えられます。すなわち１位のチームは最初から１勝を得られるのです。ファイナルステージは，先に４勝した方が勝ちとなります。もちろん１位チームの１勝のアドバンテージはカウントされます。また，ファーストステージ同様，引き分けは１位チームに有利にはたらきます。さらに１位チームはホームグランドでずっと試合が出来るのです。「ホームグランドでの試合＝常に後攻」となります。９回で決着がつかない場合は延長戦となります。延長戦は現行では最長で12回までです。延長12回で決着が着かなければ，それはすなわち１位チームの勝利に等しいのです。

さて，今年のパリーグのクライマックスシリーズは，ペナント１位のソフトバンクホークスがファーストステージを勝ち上がってきた西武ライオンズを３連勝で下しました。終わってみればソフトバンクの圧勝でしたが，試合内容はそうだったでしょうか。終盤で大差がついた試合もありましたがどの試合も接戦でした。特に最終の第３戦は，今年のプロ野球の試合の中でももっとも緊迫した試合と言えるでしょう。同点のまま延長12回までもつれ込んだその試合は，先攻の西武が12回表に得点出来ないと，その段階ですでに次の試合がない，すなわち敗退が決まります。結果，西武は得点できずソフトバンクの日本シリーズ進出が決定しました。けれども試合はまだ終わっていません。12回裏のソフトバンクの攻撃が残っていたのです。戦意喪失したであろう西武は，当たり前のように得点を許しサヨナラ負けを喫しました。西武ライオンズがソフトバンクホークスの引き立て役をしただけの12回裏の攻防でした。シリーズの勝者を決める必要があっても，試合の敗者を明確にする必要はあったのでしょうか。次の試合が決して出来ないことを承知の上でマウンドに立った西武の若き抑え投手は，どんな気持ちで投げたのでしょうか。

野球だけではありませんが，すべてのスポーツはルールに則った上で成り立ちます。野球の場合「没収試合」がある限り12回裏が終了するまでは，絶対的にソフトバンクが勝利したとは言えないでしょう。野球の場合の没収試合は，怪我などで選手の数が足りなくなったり，あるいは故意に試合を遅らせる行為があった場合に適用されます。けれども今回のクライマックスシリーズでそのようなことが起こるでしょうか？ルールだから仕方ない，と言ってしまえばそれまでですが，あまりにも残酷な幕引きにそこまでする必要があったのだろうかと感じました。日本には「武士の情け」という言葉があります。勝者を決めるためのシリーズならば，そこで試合は終了とする新たな日本式のルールがあってもいいのではないでしょうか。

11/10/10
習うよりも慣れろ

三角形の面積の求め方である(底辺×高さ÷２)という公式は小学生の頃に教わります。どんなに算数や数学が苦手な人でも，この公式を知らない人はまず居ないことでしょう。では，台形の面積はどうでしょうか。これもだいたいの人は覚えているのではないでしょうか。それくらい，日本の初等教育はしっかりしているのです。日本人において，いわゆる文盲はほとんど居ないことでしょう。現代日本人の識字率はほぼ100％に近いのです。

それはさ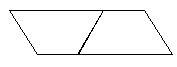ておき，先ほどの台形の面積の公式はどのようにして求めたのでしょうか？それを知るためには，台形の面積の前に平行四辺形の面積の求め方を知る必要があります。その公式は(底辺×高さ)によって与えられます。平行四辺形は一本の対角線で２個の三角形に分けることにより，三角形の面積の公式が導き出せるのです。さらに，台形は同じ形の台形を180度回転させ合体させると平行四辺形となります。その底辺が(上底＋下底)に等しくなり，それに高さを掛けます。同じ台形が２つあるのでそれらの計算結果を２で割れば台形の面積の公式が出来上がります。三角形の面積も台形の面積も，平行四辺形の面積を利用することにより導き出せます。ではその大本となる平行四辺形の面積はどのようにして得られるのでしょうか。小学校では最初に正方形や長方形の面積について学びます。その延長線上に平行四辺形が出てきます。それら四角形の面積の出し方は，小学校では詳しく教えられていないことでしょう。そもそもが小学生には理解が困難な内容なのです。習うよりも慣れろで，ドリルなどで面積の計算練習をした覚えはないでしょうか。長方形ならばまだ縦と横を掛けることによって面積が得られるのは直感的にも理解できるでしょう。では，円の面積はいかがでしょうか。さらに球の体積となるともうお手上げではないでしょうか。

平行四辺形も含め，これらの公式を正しく導くためには高等数学が必要となります。いわゆる微分積分法まで学ぶのを待つしかないのです。小学校で教わる公式を証明するために，それほど長くの時間，算数・数学を学ばなければならないのです。数学は証明の上に成り立つ学問であるとも考えられます。けれども，すべての定理や公式においてそれにこだわる必要はあるのでしょうか。将来的に数学を専門職とするのならば，そういったこだわりもいいでしょう。でも，原理や公式をある程度理解した上で問題を解いていける快感を知ることがほとんどの児童・生徒には大切なことと思います。

11/09/09
プラネタリウム

毎年夏から秋にかけて流星群が見られるといった類のニュースが聞かれます。宇宙に思いを馳せれば，その壮大さに誰しもあこがれることでしょう。学校の理科の勉強は苦手だけれども，宇宙や星のことになると目を輝かせる中学生・高校生は珍しくありません。宇宙はいつ誕生したのか，宇宙に果てはあるのか，あるいはその外側はどうなっているのか，などなどそれこそ疑問が尽きることは無いようです。その成り立ちがあまりにも広大であり，その歴史も途方も無く長いためにいまの科学の力を持ってしても，その一部しか分からないのです。人は自分の知らないことに対して「知りたい」という好奇心を持っているのです。

秋の夜長の空を眺めるのも楽しいでしょうが，実際にそうした時間を取ることが難しいのが現実でしょう。そんな人のためにプラネタリウムが有ります。プラネタリウムは現在だけではなく，過去にさかのぼったりあるいは未来の空を見ることもできます。見る場所も日本だけではなく，もし海外で見たならどんなふうに見えるのか，そんな贅沢も可能なのです。日本では見ることがかなり困難な南十字星だって簡単に見られます。タイムマシーンの機能を備えた遊覧船のようなものでしょうか。時空を超えて好きな時間，好きな場所に行けるのですから。プラネタリウムは単に星を見るだけのものではありません。季節ごとにさまざまなプログラムが組まれています。こども向けにわかりやすい解説を加えたもの，音楽と融合させた大人のためのプラネタリウムもあります。妊婦を対象とした「マタニティープラネタリウム」といったものまであるようです。目的に応じて楽しみ方も多様化しているのです。

宇宙の歴史が始まったのは約137億年前といわれています。この先宇宙はどうなるのでしょうか。現段階で推測できることは太陽の寿命とその後の太陽系のこと，銀河系とアンドロメダ星雲の衝突などです。物理学の世界でも，この先宇宙は膨張し続けるのかいつか収縮に転じるのか，決定的な見解は出ていないようです。それだけ謎が多いということでしょう。限りなく速いとされている光でさえ，宇宙空間では“鈍足”に思えることがあります。それだけ広大な宇宙をぼんやりと気軽に眺めながら，たくさんの自分の知らないことを教えてくれるプラネタリウムに，特定の目的意識も無いのに何となく足を運んでみる余裕があるくらいのゆったりした気持ちを持ち合わせたいものです。

01/08/08
学習法

学習方法にはさまざまな方法があります。昔からある伝統的なものから，個人的に編み出したものなど多岐に渡ります。そういったことを紹介している書籍も出版されています。成績のいい人のノートを紹介している本や，いまではたくさんのイラストあるいはアニメ的な絵などを表紙にして，いまどきの中高生の目を引こうとする参考書もあります。元素記号一つひとつにキャラクターを配している参考書もありました。ただ，重要でない元素までに性格をつける必要があるのだろうかとちょっと疑問を感じましたが，これも一つの学習法でしょう。

暗記物を覚えるために，家の風呂場やトイレなどに助動詞の活用表や歴史の年府，数学の公式や元素の周期表を貼っておくといった方法はオーソドックスな方でしょう。いわゆる隙間の時間を有効利用するために考えられる学習法です。こういった類のものは，参考書や受験雑誌の付録などに出来合いのものも有りますが，自分で工夫することも大事でしょう。人のつくったものでは無く，自ら考えて作成したものの方がより自分の肌に合うはずだし，必要に応じて手直しをし，やがてそれに愛着を持てるようになる頃には，おそらくその表などすでに必要ないくらい覚えていることでしょう。

学習する方法は千差万別です。大事なことは自ら考えて工夫することです。もし考えつかないのなら，最初は人の真似で構いません。それも一つの学習なのだから。自ら考えることをしなくなったら，与えられたものしか考えられないような人間になります。そこから生まれるものは，間違いなく多くは期待できないでしょう。失敗しても，下手でもいいので自ら考えてください。そうしていればいつかは新たに何かが生まれてくるのだから。

11/07/07
ライバル

学習効果を考えた場合，先生が一人に対して生徒が一人，いわゆる一対一で行うことが良しとされることは多いようです。他の生徒に邪魔されずに，一人の先生を占有でき自分の学びたいことを主に教わることが出来るのだから，そう思うのは当然かも知れません。ピアノやバイオリンなど，楽器のレッスンにしても，複数の生徒が同時に教わることが好ましいとは言えないでしょう。けれども，あらゆるケースでそれは正しいでしょうか？

ある企業で新しいプロジェクトを企画したとき，中心となって企画を進める役にお互いライバル視している二人を指名したことがありました。二人は同期で，ことあるごとに競い合い他方に負けることを何よりも嫌っていました。傍目からは誰にも二人の中が悪いことは分かっていました。まったく息の合っていないそんな二人に，重要な企画を任せていいのかとまわりは気掛かりでした。上司の配置ミスではないかと言う声も囁かれたようです。そんな心配をよそに，企画は見事に成功しました。もちろん結果を残すまでには紆余屈折があったことでしょうが，意見を対立し合いながらもプロジェクトを成し遂げようとした二人が居たからこそ成り立った仕事だったのです。

運動競技などでもライバルの存在の有無によって，選手の記録が伸びることがあるようです。それはたとえば同じ学校の中だけでのライバルでも，他校の人でもいいのです。あるいはもっと広く，海外の選手のライバルが居れば世界記録に関わるまで記録に関与してくるかもしれません。そこまで話を大きくしないまでも，小さな社会の中でも同様のことはあり得ます。競い合うもう一人が居る。それはこどもの学習において，この上ない向上の要因となるのです。

11/06/06
継続すること

人は気に掛かったことが解決しないと気が済まない人と，あまり気にせずに過ごしてしまう人の２つのタイプに大別できます。もちろんその度合いに個人差があるので，どちらかに近い傾向をもつと言った方がいいかもしれません。学者肌の人などは前者の方でしょう。ある学者の話です。長い間研究している問題がありました。研究に研究を重ねながらも，その糸口はつかめませんでした。ところがある日バスに乗ろうとステップに足を掛けた瞬間にひらめいたそうです。バスに乗るタイミングが問題解決とはまったく関係ないことは言うまでもありません。大事なことはいかに継続して考えていたかでしょう。考えるのをやめてしまったらおそらく研究課題を解決することはなかったでしょう。継続して考える，ということがここでは重要なことです。

専門職としてそこまで深く入り込まないまでも，ふだんからの自分に置き換えた場合はいかがでしょうか？疑問が生じたときに調べる時間が無い，あるいは面倒くさく思い「まあいいや」と言い訳しながら過ごしてはいないでしょうか。少し前にテレビで豆知識を取り上げた番組がありました。いわゆるトリビア的なものです。英語の“trivia”は「ささいなこと，つまらないこと」と訳されます。けれどもささいでつまらない知識も蓄積していけば後に役に立つものです。その知識を系統立ててまとめ上げれば，それはもう立派な知の財産となることでしょう。

大学の教授が授業中に自分の研究課題についてひらめいたときが非情に辛いと言っていました。その場ですぐに取り組みたいものの，授業は続けなければなりません。あとで取り組もうとしても思い出せないのです。そのときに思いついたとしても，あとで思い出せない。誰でも経験のあることでしょう。忘れないためにはその場でメモを残すことが大事ですが，研究課題のように深く入り組んでいる場合ともなると，そうも行かないのかもしれません。それでも常に考えを巡らしていれば，いつかは解決へと辿り着けることでしょう。少なくとも考えなくなってしまったらそれでお終いなのですから。

11/05/05
道具

専門家が使う道具にはこだわりを持つ人が多いことでしょう。プロ野球選手のバットは毎年のようにバット職人と打ち合わせをして，グリップの形状や重さ，重心の位置など綿密に決めているようです。陸上選手のスパイクなどは，その出来如何で競技結果に直接反映されることでしょう。競泳競技においては水着の素材により記録が著しく変わり物議をかもしたことは記憶に新しいことです。選手の努力とは別の次元で記録がどんどん生まれるのは，確かにタイムを争う競技としては好ましいことではありません。100分の１秒でも速く泳ぐことに日々練習している選手にとって，水着＝道具によって記録が変わってしまうのは不本意なことでしょう。道具に左右されてはいけない一例でしょう。

床屋で使うハサミがかなり高額であることを聞いたことがあります。家庭で使うハサミの値段は数百円程度が常識的な価格でしょう。5000円を超えるハサミを持っている人はあまりいないのではないでしょうか。ところがプロが使うハサミ＝道具は桁が違います。自分の手先が生命線である職種においては道具は特に大事なものなのでしょう。音楽家における楽器，書道家の筆や硯など芸術家にとっての道具はもはや体の一部とさえ思えるほどです。

そこまで極端ではないものの，市井の人でもそれなりに道具にこだわることもあるでしょう。ものを書くことが多い人ならば筆記用具に凝ることがあります。万年筆の愛好家から，必要性もないのに次はどんな万年筆を買おうかと思うようになると“はまっている”状態だと聞いたことがあります。コーヒーや紅茶の愛好家ならカップを選び，ビール好きならばその日の気分によってグラスを決めるのも楽しいことでしょう。道具と言うほどではありませんが，お気に入りの傘を一本持っているだけで，憂鬱な雨の日に出掛けることが少しだけ楽しみになることもあります。こだわりに一品を持つことは，ふだんの生活を少しだけ豊にするはずです。

11/04/04
研修

毎年四月になると，電車内や街のあちこちで新入社員の姿を見かけます。真新しいスーツを着ているのですぐに分かります。まだ学生気分も十分に抜けきれないまでも，新しい生活に不安と期待を抱きながら過ごしていることでしょう。新人の最初の仕事は，上司や同僚の顔と名前を覚え，先輩に連れられて取引先に挨拶に行ったり，商品の特徴や売り込みなどを勉強をすることでしょう。

一般企業では新入社員を対象とした研修が行われるのが通常です。研修期間やその規模は会社によって差こそあることでしょうが，いわゆる右も左も分からないような新人は，教官や先輩に教わることによって仕事を覚えていきます。新人教育に要する時間と費用はそれ相当のものが必要で，新人を育てている間は企業にとっての直接的な利益はありません。あくまでも将来に対する投資であり，新人が戦力と成るまでは支出ばかりが計上されることでしょう。そこまでしてでも人を育てるということは，それが企業にとって必要不可欠だからです。

ところで学校の現場はどうでしょうか。新任の先生がいきなり教壇に立つことなど決して珍しくありません。学生時代に塾講師や家庭教師さえしたことのない先生も居ることでしょう。仮にそういった経験があるにしても，学校のように大人数での一斉授業を経験している人は少ないことでしょう。中にはいきなり担任を任されたということも耳にします。担任を持つことは，授業をすること以外でも多忙となります。その結果，授業準備もままならないまま授業に臨むことになります。授業がおろそかになると生徒からの信頼も揺らぎ，やがて学級崩壊やいじめなどの問題が発生することは容易に想像できます。

学校教育においても新人教育は必要です。少なくとも最初の一年間はベテランの先生につくなどして，授業の進め方やクラス運営，教務や実務など教わらなければなりません。研修会なるものは行われているようですが，それが本当の意味での学校教育にどれだけ即しているのでしょうか。教育の現場にほとんど携わったことのない，『学生』にいきなり感受性の強い時期のこども達と対峙するのは困難です。結果，先生としての適応力が無いと「上」の人に判断され，不本意な思いをして教師を辞めていく若者が出てしまうことでしょう。新人を育てていくことは大変です。けれどもそれは必要なことです。学校現場でも，一年間じっくりと研修を行い，戦力となる先生を育てるべきです。

11/03/03
月明かりの中で

原作のある映画の宣伝文句で「読んでから見るか，見てから読むか」といったキャッチコピーが以前ありました。先に原作を読むと，映画の結末が分かってしまい，クライマックスの楽しみが半減してしまいます。その逆に映画を見てから原作を読むのも似たようなことが言えるでしょう。ただ，映画よりも本の方が細かい設定や，物語の背景などのティテールにこだわるでしょうから，映画を見たあとでも十分楽しめるかも知れません。映画を見たときには不可解だったことが，あとで明らかになってくるとしたならば二度楽しめることでしょう。ときには映画が原作と違いすぎて，批判の対象になることもあります。原作と映画，どちらが先かという議論はたいてい二分してしまい，その結論を出すことは困難というよりも不可能でしょう。それはどちらの主張も決して間違ってはいませんが，絶対的に正しいという論拠もないからです。数学における命題とは異なるのです。

人は目に見えているものを認識し，それをもとにさまざまなことを感じ思いを巡らせることが出来ます。現実に見えているものが真実であり，判断の基準となるのです。もちろんそれは間違っていません。経験則としてそう過ごしてきたのですから。もっとも見たものだけしか信じられない人も居れば，自分が信じたものだけしか認められない人が居るのも事実です。映画と原作の順序ではありませんが，これも真となる答がないのです。それはさておき，順序がいずれであっても原作を読むとことによりその物語の深みを感じられるのは間違いないことでしょう。

いまの世の中，分からないことが有ればネットや電子辞書などで簡単に調べられます。便利になった分，答えに至までの“考える”という楽しみが無くなってしまいました。思考過程によってでしか得られない喜びもあるはずです。目に見えるものがすべてではないのかも知れません。明るい電灯のもとばかりでものを見たり考えたりするのではなく，ときには月明かりの中で静かに物思いにふけるのも，決して無駄な過ごし方ではないでしょう。

11/02/02
保険

自動車を所有している人は誰でも保険に入っていることでしょう。強制的に義務づけられている自賠責保険以外にも，保険会社が提供しているさまざまな保険に，ほとんどすべての人が加入していることでしょう。それほど車の運転にはリスクが付きまとうからです。その保険の中にも，対人・対物保険や搭乗者保険，車両保険など内容はさまざまで，補償金額を無制限にするか，保険料を抑えるためにある一定の金額にするかなど，それこそ個人個人によって千差万別でしょう。

生命保険や健康保険なども，成人し社会人ともなれば加入するのが普通でしょう。特に生命保険はその保険金額がかなり大きくなるので，どういった種類の保険に入るのか，あるいはどのくらいの保障を考えるのか悩ましいところです。種類が多い上に，素人にはその仕組みが難しく理解するにはなかなかおよびません。手続きの面倒さや，契約書の文字の細かさなど，ちょっと近寄りがたいものがあります。保険商品も年々新しくなり，また自分の生活スタイルや家族への責任，地位などで状況もがらりと変わることさえあります。病気になってから，あるいは災害にあって家を失ってから保険に加入していなかったことを後悔しても遅すぎるのです。

保険はいわゆる「転ばぬ先の杖」であるのですが，誰だって自分が不幸に襲われることなど望むはずもありません。それでも何かに苛まれてしまうのが人生です。若いうちにはそういったことは実感できないかも知れません。「芸は身を助ける」とも言います。芸とは習って身につけることです。この先役に立つとか立たないとかではなく，いま必要とされていることが出来ない人は，この先も同じようなことをくり返す。そんなふうに考えが及ぶようになれば，先を見通す目を養うことも可能でしょう。 　

11/01/01
サービス業

年末に大掃除をした人はどれくらい居たでしょうか。ふだんの掃除ではしないところまで手を掛けることがあるのが大掃除なので，それなりに時間と手間が掛かったことでしょう。ギトギトになった換気扇や，カビの生えてしまった風呂場の隅など出来ればやりたくない，そんな本音を漏らした人も居るのではないでしょうか。こうした掃除を代行してくれる業者もあるようです。サービス業者には自分では出来ないことあるいはやりにくいことを代わりにやって貰い，その代償として代金を払います。

正月に欠かせないのがおせち料理です。ところがこのおせち料理をきちんと作っている家庭はほとんど皆無ではないでしょうか。ある程度は作っても，数の子や栗きんとんなどは出来合のものを買ってくる人が多いのではないでしょうか。それだけ手間ひまが掛かり，面倒を感じるのでしょう。あるいは家庭でつくる習慣が，いまの若い世代にはすでにほとんど無くなってしまったのが実情でしょうか。いまの時代は正月が近づくと，デパートやスーパーにはおせち料理が所狭しと並び，ふだんの食材はどこかへ追いやられてしまいます。最近ではコンビニエンスストアや宅配でのおせち料理を提供するサービスもあるようです。家庭で出来ないあるいは出来にくくなったことを代行しその代価を得るというサービスを，デパートや料理屋が代行するのです。

家庭でもある程度の年齢まではこどもの勉強をみることが出来ます。ところが学年が上がると共に，それが困難になるのが普通でしょう。内容的なものが難しくなることと，両親の仕事や家事が忙しくなることにその要因があるでしょう。勉強の代行をするのが塾や家庭教師です。サービス業にはいくつもの同業他社が存在します。その中での競争原理によりサービスの向上がみられます。塾もサービス業である限り，どこよりも質の高い講師と授業が求められるのは当然です。授業料を支払う親の目も厳しいけれども，授業を受けるこども達はそれ以上に先生のことをみているはずなのですから。サービスを提供する側の質を向上させるために，講師も塾自体も常に向上する気持ちを持たなければなりません。